

Here are a few calculators for electronic/radio circuits. They are quite crude, but they work. Note that these formulas now accept "floating point" variables (an inductance value of 0.01 is a valid number).

Just add them together!

Formula: Effective Resistance = (R1 x R2) / (R1 + R2)
(all units are the same, Ohms/Farads etc.)

Formula: Reactance = 1 / (2 * Pi * F * C)

I have included a few calculators here. Each time you see the text [Enter] you are being asked to enter data in the field. If you have previously used another calculator then there will already be default start values entered for you. These are the results of your previous calculaton. You may of course enter new values.

C1, C2 and C3 are all in series and so form a single tuning capacitor of about 60pf. The ratios of C2:C3 determine the gain and their values may vary quite a lot. In general, C2 = 3x wavelength, C3 = 9x wavelength. C1 can be any value from 1x wavelength to 10x wavelength and is normally chosen to fine-set the frequency of the oscillator. Make C1 start value about the same as C2. The actual values can vary over quite a wide range. This calculator will calculate the total tuning capacitance for your own selected values.
In the above calculator, enter a frequency and click the "SHOW C1, C2 & C3" button and the values of C1, C2 & C3 will be displayed. If you then click the "SHOW CAPACITANCE" button, you will see the value of the effective tuning capacitor that will be resonated with L1. You may also enter your own C1, C2 and C3 values to find the effective tuning capacitor that will be resonated with L1.

The inductor L1 resonates with the total capacitance above to determine the operating frequency. If you know the capacitance, having just read the the previous chapter, then use your basic frequency (transposed) to give inductance, or plonk your values in this little calculator:

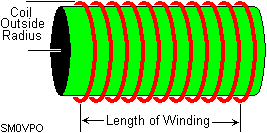
Now you know the inductance and the capacitance, it is just to buy and insert those values into the circuit. But if you really want to wind the coils yourself, then you will probably use either air-cored 6mm Dia. formers, or use formers with a ferrite core. There are precise formulas to use but I like this method. Insert the required inductance and click the button.
Please remember that this last "calculation" is very approximate since a lot depends upon the individual former. The "Ferrite core" is assumed to be a re-wound IF can.

Formula: Reactance = 2 * Pi * F * L

Formula: Frequency (F) = 1 / (2 * Pi * Sqrt(LC))

| Formula: |  |
 |

| Formula: |  |
 |

Calculates the effective temperature rise coefficient of a measured heatsink. Area is EXPOSED surface area of heatsink in square centimeters.
| Formula: | Degrees Centigrade per Watt = 50 / Sqrt(Area sq-cm ) |

Calculates heatsink surface area needed for a given heatsink temperature coefficient.
| Formula: | Area Required (sq-cm) = Sq (50/C-watt) |


| Formulas: |  |
The Input/Output powers may be in any electrical unit you prefer, eg: Meggawatts, Picowatts, Joules, Hamster-treadmill revolutions per hour etc.
Negative values of resistance occur when impossible values of input and output impedance and attenuation are entered. For example, it is not possible to drive a 50-ohm line from a 600-ohm line and have a voltage attenuation factor of less than 6.78


| Formulas: |  |
The Input/Output powers may be in any electrical unit you prefer, eg: Meggawatts, Picowatts, Joules, Hamster-treadmill revolutions per hour, etc.
Again, negative values indicate an impossible attenuation situation.

